10. Sınıf Matematik Beceri Temelli Etkinlik Kitabı Sayfa 77 Cevapları Meb Yayınları‘na ulaşabilmek ve dersinizi kolayca yapabilmek için aşağıdaki yayınımızı mutlaka inceleyiniz.
10. Sınıf Matematik Beceri Temelli Etkinlik Kitabı Cevapları Sayfa 77
Selçuklu kültür ve medeniyetinin temel figürlerinden biri sekiz köşeli yıldızdır. Birçok tarihi eserde görülen ve günümüz mimarisinde de sıkça kullanılan bu figür, biri diğerinin ağırlık merkezi etrafında 45 derecelik açıyla döndürülmesi sonucu elde edilen iç içe geçmiş iki kareden oluşmaktadır. Bu sekiz köşeli yıldızın her bir köşesi erdemli bir insanın sahip olması gereken ilkeleri simgelemektedir.
Bu bilgiden etkilenerek işe koyulan bir çini ustası bir kenar uzunluğu 2+^2 birim olan kare şeklinde bir kalıp oluşturur. Bu kalıp ile bir kare çizen usta, karenin merkezini değiştirmeden kareyi 45 derece döndürerek bir kare daha çizer. Çini ustası böylece Selçuklu yıldızı figürünü oluşturur. Sonra kenarları ilk çizilen kareye paralel, bir kenarının uzunluğu, döndürülerek oluşturulan karenin köşegen uzunluğuna eşit ve ağırlık merkezi, oluşturulan yıldız figürüyle aynı olan beyaz renkli bir kare fayans üzerine bu figürü çizer. Yıldızın oluşturduğu bölgeyi de mavi renge boyar.
Yukarıda verilen bilgilere göre aşağıdaki soruları cevaplayınız.
Fayans üzerine işlenen yıldız figürünü oluşturan karelerin tüm kenarlarına siyah bir hat çekilirse hangi düzgün çokgenler elde edilir?
- Cevap:
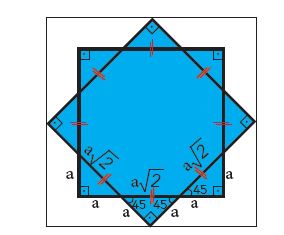Oluşan sekiz tane eş ikizkenar dik üçgenin dik kenar uzunluklarından her birine a denilirse düzgün sekizgenin bir kenar uzunluğu a√2 br olur. Oluşan eş karelerin bir kenar uzunluğu 2a + a√2 br olacağından 2a + a√2 = 2 + √2 olur. Böylece a = 1 br bulunur.
İki kare ve bir düzgün sekizgen elde edilir. (Oluşan üçgenler eşkenar üçgen olmadığı için düzgün çokgen değillerdir.)
Fayans üzerine mavi boya ile işlenen Selçuklu yıldızı figürünün alanı kaçtır?
- Cevap:
Yıldızın alanı = (2 + √2)2 + 4 – (1•1/2)
= 4 + 4√2 + 2 + 2
= 8 + 4√2 br2 olarak bulunur.
Fayans üzerindeki beyaz renkli bölgenin alanı kaçtır?
- Cevap:
En dıştaki büyük karenin (fayansın) bir kenar uzunluğu, içteki küçük eş karelerin köşegen uzunluğu kadar olup 2 + 2√2 birimdir.
Beyaz bölgenin alanı = Fayansın alanı – Yıldızın alanı
(2 + √2)2 – (8 + 4√2)
= 4 + 8√2 + 8 – 8 – 4√2
= 4 + 4√2 br2 olarak bulunur.
10. Sınıf Meb Yayınları Matematik Beceri Temelli Etkinlik Kitabı Sayfa 77 Cevabı ile ilgili aşağıda bulunan emojileri kullanarak duygularınızı belirtebilir aynı zamanda sosyal medyada paylaşarak bizlere katkıda bulunabilirsiniz.
